Greg Parker G and Charlton M are in the Department of Electronics and Computer Science, University of Southampton, Highfield, Southampton SO17 1BJ, UK
We can now buy personal computers that operate at 1 GHz (109 Hz), which is very impressive, but what is the likelihood of a 100 GHz desktop computer appearing on the market? Indeed, given our current understanding of semiconductor technology, even producing a 10 GHz personal computer would seem to be difficult. However, by transmitting signals with light rather than electrons, it might be possible to build a computer that operates at hundreds of terahertz (1012 Hz). Researchers now believe that such an awesome processing engine could be built from optical components made from so-called photonic crystals and quasicrystals. These materials have highly periodic structures that can be designed to control and manipulate the propagation of light.
Basics of photonic band gaps
The easiest way to understand the behaviour of light in a photonic crystal is to compare it to the movement of electrons and holes in a semiconductor. In a silicon crystal, for example, the atoms are arranged in a diamond-lattice structure, and electrons moving through this lattice experience a periodic potential as they interact with the silicon nuclei via the Coulomb force. This interaction results in the formation of allowed and forbidden energy states. For pure and perfect silicon crystals, no electrons will be found in an energy range called the forbidden energy gap or simply the band gap. However, the situation is different for real materials: electrons can have an energy within the band gap if the periodicity of the lattice is broken by a missing silicon atom or by an impurity atom occupying a silicon site, or if the material contains interstitial impurities (additional atoms located at non-lattice sites).
Now consider photons moving through a block of transparent dielectric material that contains a number of tiny air holes arranged in a lattice pattern. The photons will pass through regions of high refractive index - the dielectric - interspersed with regions of low refractive index - the air holes. To a photon, this contrast in refractive index looks just like the periodic potential that an electron experiences travelling through a silicon crystal. Indeed, if there is large contrast in refractive index between the two regions then most of the light will be confined either within the dielectric material or the air holes. This confinement results in the formation of allowed energy regions separated by a forbidden region - the so-called photonic band gap. Since the wavelength of the photons is inversely proportional to their energy, the patterned dielectric material will block light with wavelengths in the photonic band gap, while allowing other wavelengths to pass freely.
It is possible to create energy levels in the photonic band gap by changing the size of a few of the air holes in the material. This is the photonic equivalent to breaking the perfect periodicity of the silicon-crystal lattice. In this case, the diameter of the air holes is a critical parameter, together with the contrast in refractive index throughout the material.
Photonic band gap structures can also be made from a lattice of high-refractive-index material embedded within a medium with a lower refractive index. A naturally occurring example of such a material is opal. However, the contrast in the refractive index in opal is rather small, which results in a rather small band gap.
The potential of photonic-crystal structures was first realized in 1987 by Eli Yablonovitch, then at Bell Communications Research in New Jersey. A few years later in 1991, Yablonovitch and co-workers produced the first photonic crystal by mechanically drilling holes a millimetre in diameter into a block of material with a refractive index of 3.6. The material, which became known as "Yablonovite", prevented microwaves from propagating in any direction - in other words, it exhibited a 3-D photonic band gap. Other structures that have band gaps at microwave and radio frequencies are currently being used to make antennae that direct radiation away from the heads of mobile-phone users.
In spite of this success, it has taken over a decade to fabricate photonic crystals that work in the near-infrared (780-3000 nm) and visible (450-750 nm) regions of the spectrum. The main challenge has been to find suitable materials and processing techniques to fabricate structures that are about a thousandth the size of microwave crystals.
A rough estimate of the spacing between the air holes (or the lattice size) is given by the wavelength of the light divided by the refractive index of the dielectric material. The problem in making small structures is compounded because it is more favourable for a photonic band gap to form in dielectrics with a high refractive index, which reduces the size of the lattice spacing even further. For example, suppose we wanted to create a photonic crystal that could trap near-infrared light with a wavelength of 1 µm in a material with a refractive index of 3.0. We would have to create a structure in which the air holes were separated by about 0.3 µm - an extremely difficult task. If the scale was 1000 times smaller, we could build the structure atom-by-atom using a chemical reaction; and if it was 1000 times larger we could build the structure mechanically, as Yablonovitch and co-workers did.
To be able to create photonic crystals for optical devices, we need to use state-of-the-art semiconductor-microfabrication techniques with their associated high production costs and investment. For this reason computer modelling of prospective photonic-crystal structures is also a very important area of research, as it may prevent expensive fabrication errors later.
Optical communications
So why are photonic crystals generating so much interest? Again it is useful to draw analogies with silicon. The current explosion in information technology has been derived from our ability to control the flow of electrons in a semiconductor in the most intricate ways. Photonic crystals promise to give us similar control over photons - with even greater flexibility because we have far more control over the properties of photonic crystals than we do over the electronic properties of semiconductors. Given the impact that semiconductor materials have had on every sector of society, photonic crystals could play an even greater role in the 21st century, particularly in the optical-communications industry.
In current communications systems, audio or video signals are encoded as streams of digital data packets. These voltage pulses are applied to a light-emitting diode (LED) or a semiconductor laser, which converts them into short pulses of light that are then sent along an optical-fibre network. Many different conversations or video signals can be transmitted using a single wavelength of light by interweaving the data packets from different sources, a technique known as time-division multiplexing. The optical data pulses are sorted at the receiving end of the fibre, where they are converted by photodetectors into continuous analogue electrical signals that are then transmitted along copper wires.
A simple way of increasing the amount of data that can be transmitted by a single optical fibre is to make the incoming electronic pulses as short as possible. Current optical systems have achieved data rates in excess of 40 gigabits per second. But to increase this value significantly will require cheap, bright LEDs that can be switched on and off at very high speed.
Another way to increase the capacity of the fibre is to add new signals at other optical wavelengths, a method known as dense wavelength division multiplexing (DWDM). However, the optical fibre is only transparent over a small range of wavelengths, so the number of separate conversations that can be transmitted depends on the linewidth of neighbouring optical channels (which is currently at the sub-nanometre level). Encoding and sorting thousands of such channels poses quite a problem: at the transmitting end of the system, each wavelength channel requires a very stable light source that only emits in a very narrow range of wavelengths. Although LEDs offer high switching speeds, they emit light over a wide range of wavelengths, which makes them less suitable than lasers for DWDM systems.
At the receiving end, very narrow linewidth filters and optical switches are required to separate individual channels and then route them to the appropriate destinations. Due to the large number of individual components in a DWDM system, it makes sense to combine as many of them as possible onto an "integrated" optical chip. This would reduce both the amount of costly manual work that is needed to build the system and the number of possible points where it could fail.
Such integration, however, raises other problems. First we need to develop small-scale optical "interconnects" - tiny planar waveguides that can steer light round tight corners. While it is straightforward to route electrons round sharp bends in microchips, it is impossible to direct light in the same way using conventional glass waveguides because the losses at the bends are so large.
Photonic crystals could address many of the problems that currently limit the speed and capacity of optical-communications networks. For example, these structures could be used to create novel LEDs and lasers that emit light in a very narrow wavelength range, together with highly selective optical filters that could be integrated on a chip.
Light-emitting diodes play a key role in optical-communication systems. These devices are made from so-called photoemissive materials that emit photons once they have been excited electrically or optically. These photons are typically emitted in many different directions and also have a range of wavelengths, which is not ideal for communications applications. We can create an LED that only emits light in the forward direction by placing a reflector behind the photoemissive layer. However, the efficiency of such a device is limited by the efficiency of the reflector.
Photonic crystals could be used to design a mirror that reflects a selected wavelength of light from any angle with high efficiency. Moreover, they could be integrated within the photoemissive layer to create an LED that emits light at a specific wavelength and direction.
A far simpler method of producing 3-D band gaps at very short wavelengths has been pursued by Judith Wijnhoven and Willem Vos at the University of Amsterdam. The technique relies on the self-arrangement of sub-micron-sized silica spheres in a colloidal suspension. However, the rather low refractive index of the silica relative to air means that the refractive-index variation across the lattice is not high enough to create a truly 3-D photonic band gap. The team has overcome this limitation by filling the air voids between the spheres with a titania-dioxide solution, which has a high refractive index. The solution undergoes a chemical reaction that causes solid titania to form. This process is repeated several times and the silica spheres are finally dissolved to leave a close-packed lattice of spherical air voids in a titania matrix (figure 1b).
Meanwhile, John Holtz and Sanford Asher of the University of Pittsburgh in the US have fabricated "tunable" photonic crystals from a suspension of polymer spheres in a hydrogel film, a synthetic polymer that absorbs water. In this case, the wavelength of the band gap can be adjusted by shrinking or expanding the hydrogel. However, although colloidal structures are easy to make and overcome the problem of scale in a very clever way, it is not easy to incorporate them within the active heterostructure of an LED.
Fortunately 2-D periodic lattices exhibit some of the useful properties of a truly 3-D photonic crystal, and are far simpler to make. These structures can block certain wavelengths of light at any angle in the plane of the device, and can even prevent light entering from certain angles in the third dimension (i.e. perpendicular to the surface). Thus 2-D photonic crystals are a good compromise for many applications and are easily incorporated within planar waveguides.
Microcavities in photonic crystals
Photonic crystals built from photoemissive materials, such as III-V semiconductors and glasses doped with rare-earth atoms, can also be used to make narrow-linewidth lasers that could potentially be integrated with other components in an optical-communications system. The lasers are made by introducing a small number of holes that are slightly smaller or larger than the other holes in the photonic-crystal lattice. These "microcavities" generate a narrow so-called defect mode within the photonic band gap.
While the material emits light in a wide spectral range, only the wavelength that matches the wavelength of the defect mode is amplified because it can propagate freely through the material. The laser cavity is formed either by the crystal facets or by external mirrors that surround the glass. The intensity of the propagating light increases as it undergoes successive reflections and travels back and forth through the photonic crystal. Meanwhile, light at other wavelengths is trapped within the photonic crystal and cannot build up. This means that the laser light is emitted in a narrow wavelength range that is directly related to the diameter of the microcavity divided by the diameter of the regular holes. Moreover, the linewidth can be reduced further by using unusual geometries of the photonic-crystal lattice.
Such microcavities are also much more efficient at trapping light than the cavities formed in semiconductor diode lasers since there are fewer directions in which the photons can escape from the cavity.
The rate of photoemission in an active medium can be greatly increased by maintaining a high optical flux density. Since microcavities act as light traps, they provide a good method of enhancing the rate of photoemission in LEDs, and are crucial for the operation of lasers. Moreover, the increased rate of photoemission means that microcavity LEDs and photonic-crystal lasers can be switched on and off at far greater speeds compared with conventional devices, which could lead to higher data-transmission rates and greater energy efficiency. Indeed, such devices are the subject of intense effort within the field of optoelectronics.
Preliminary experiments have been performed at microwave frequencies on defect structures within photonic crystals made from "passive" materials that do not emit light. Recently John Joannopoulos and colleagues at the Massachusetts Institute of Technology (MIT) in the US have demonstrated very strong photon confinement within a simple 1-D microcavity made by etching a single row of holes onto a narrow silicon waveguide.
Photonic-crystal microcavities that are fabricated from passive materials, such as silicon dioxide and silicon nitride, could also be used to create filters that only transmit a very narrow range of wavelengths. Such filters could be used to select a wavelength channel in a DWDM communications system. Indeed, arrays of these devices could be integrated onto a chip to form the basis of a channel demultiplexer that separates and sorts light pulses of different wavelengths.
Although complex photonic-crystal LED and laser structures are being developed, fundamental questions about the formation, operation and efficiency of photonic band gaps remain unanswered. Real photonic-crystal waveguides are far from ideal because they suffer losses due to diffraction and scattering, and due to an optical mismatch at the surface joining the device to input and output waveguides. These loss mechanisms need to be fully understood and the devices need to be optimized for particular wavelengths before they can become commercially viable.
Passive materials provide a good testing ground to investigate these factors. Our group at Southampton University is studying the physics underlying band-gap formation, verifying computational-design methods experimentally, and developing integrated optical filter and switching devices.
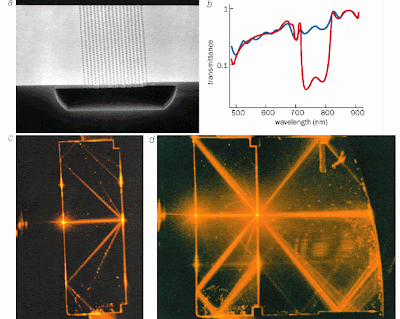
(a) This photonic waveguide formed from a thin silicon-nitride membrane contains a triangular lattice of air holes separated by 300 nm. The air gap below the waveguide leads to stronger photon confinement. (b) A plot of transmission versus wavelength for the device shows that it has a photonic band gap between 725 nm and 825 nm if the electric field associated with the electromagnetic wave is perpendicular to the direction in which the light wave propagates (red). In contrast, the light can pass freely through the material when the magnetic field is perpendicular to the direction of travel (blue). In this case, the photonic band gap is said to be incomplete. (c) A photonic crystal made from a piece of silicon approximately 1 x 1.5 cm viewed from above. Laser radiation with a wavelength that lies inside the band-gap range enters the structure from the left and is completely blocked. (d) Light at longer wavelengths outside the band gap can pass through the structure.
For example, we have built a photonic-crystal device that works as a simple filter (figure 2). The device was created by growing a thick layer of silicon dioxide on the surface of a silicon substrate, followed by a layer of silicon nitride. The positions of the holes were defined by patterning the top surface of the waveguide with electron-beam lithography. The underlying silicon dioxide was then etched away to create a free-standing porous silicon-nitride membrane that blocks light over the wavelength range 725-825 nm. Similar devices were also fabricated with band gaps at shorter visible wavelength. Although it is more challenging to fabricate photonic crystals at optical wavelengths, it is easier to conduct experiments with them due to an abundance of visible-light sources and detectors.
Quasicrystals overcome losses
Real photonic crystals experience losses due to the mechanisms described earlier. Such losses are not a problem for active laser devices in which a large amount of optical radiation is generated and then coupled directly to an optical fibre pressed against it. In contrast, passive devices are typically used to filter a weak optical signal that may have travelled through hundreds of kilometres of optical fibre - in this case it is crucial to keep any further losses to a minimum.
As well as the fundamental problem of transferring the light from a waveguide into a photonic-crystal filter, unwanted back reflections from the filter must also be minimized as they reduce the size of the signal pulse and may lead to errors in the high-speed optical links.
One way to reduce reflections would be to reduce the refractive index of the materials from which the photonic crystal is fabricated. However, this creates something of a paradox since the formation of the photonic band gap is largely governed by the contrast in refractive index between the materials.
Nevertheless, since photonic crystals are artificial structures, we are at liberty to change the geometric parameters to compensate for the reduction in refractive index. The band gap can be restored in materials with a low refractive index by increasing the number of degrees of symmetry in the lattice.
For example, a rectangular arrangement of air holes etched into a silicon block has twofold symmetry. In other words, photons travelling along the length of the photonic crystal experience a different hole spacing from photons travelling at right angles within the plane of the material. This means that the photonic band gap changes depending on the direction in which the light travels, and it may disappear altogether in some cases. However, if a triangular lattice arrangement - which has sixfold symmetry - were used instead, light from any direction in the plane of the material would experience the same photonic band gap.
Interconnects for optical circuits
Miniature waveguides that could be used to transmit light signals between different devices are a key component for integrated optical circuits. However, the development of such small-scale optical interconnects has so far been inhibited by the problem of guiding light efficiently round very tight bends.
Conventional optical fibres and waveguides work by the process of total internal reflection. The contrast in refractive index between the glass core of the fibre and the surrounding cladding material determines the maximum radius through which light can be bent without any losses. For conventional glass waveguides this bend radius is about a few millimetres. However, the interconnects between the components on a dense integrated optical circuit require bend radii of 10 µm or less.
It is possible to form a narrow-channel waveguide within a photonic crystal by removing a row of holes from an otherwise regular pattern. Light will be confined within the line of defects for wavelengths that lie within the band gap of the surrounding photonic crystal. Since a porous material has no available modes at this wavelength, an optical quantum well forms in the waveguide region and traps the light. Under these conditions we can introduce a pattern of sharp bends that will either cause the light to be reflected backwards or directed round the bend. Joannopoulos and colleagues at MIT have shown theoretically that the light will be guided round the bend suffering little, or even zero, loss due to back reflectance.
We have recently tested these ideas experimentally on a photonic-crystal beam splitter that we designed and built at Southampton (figure 4). We defined a wide Y-shaped "defect waveguide" within the photonic crystal by removing some of the holes from the lattice. This device showed that a small amount of light was in fact guided round the bend, although the losses were quite high. However, the photonic crystal was found to modify the spectral properties of the transmitted light in a beneficial way. For example, the amount of light reflected back from the pointed corners was reduced. We are currently investigating methods to optimize these structures.
Materials with photonic band gaps could speed up the Internet by improving the transmission of long-distance optical signals. One drawback with conventional optical fibres is that different wavelengths of light can travel through the material at different speeds. Over long distances, time delays can occur between signals that are encoded at different wavelengths. This phenomena - known as dispersion - is worse if the core is very large, as the light can follow different paths or "modes" through the fibre. A pulse of light travelling through such a fibre broadens out, thereby limiting the amount of data that can be sent.
These problems could be solved by an extremely unusual "holey fibre" developed by Philip Russell and Jonathan Knight of the University of Bath and co-workers. The fibre has a regular lattice of air cores running along its length and transmits a wide range of wavelengths without suffering from dispersion. It is made by packing a series of hollow glass capillary tubes around a solid glass core that runs through the centre. This structure is then heated and stretched to create a long fibre that is only a few microns in diameter. The fibre has the unusual property that it transmits a single mode of light, even if the diameter of the core is very large.

Future outlook
Predictions are always difficult to make - however, the future for photonic-crystal circuits and devices looks certain. Within five years a number of basic applications will start making an appearance in the market-place. Among these will be highly efficient photonic-crystal lasers and extremely bright LEDs. On the same timescale we hope to have demonstrated the feasibility of using photonic-crystal waveguides to route light round micron-sized optical benches, and the use of photonic crystals for high-resolution spectral filtering. These demonstrators may be combined to produce a commercially viable "spectrometer on a chip" within a ten-year timescale. Meanwhile, circuits of a similar complexity - including "add-drop filters" and Mach-Zehnder interferometers, common components in optics - will be available at about the same time.
By the time every home is connected to an optical-fibre network, "set-top boxes" that sort and decode the signals will contain photonic-crystal circuits and devices rather than cumbersome optical fibres and silicon circuits. And on a five- to ten-year timescale we should have demonstrated the first photonic- crystal "diodes" and "transistors". A demonstration of the first photonic- crystal logic circuit could even take place in the next 10 to 15 years, while a prototype optical computer driven by photonic crystals could be available within the next 25 years. Surprisingly, synthetic opals could even find a niche in the valuable jewellery and artwork markets, while thin photonic-crystal films could also be used as anti-counterfeit devices on credit cards.
If our predictions are hopelessly awry, by then we hope that most people will have forgotten we made them. Nevertheless the future for photonic crystals looks bright.
Further reading
M D B Charlton, S W Roberts and G J Parker 1997 Guided mode analysis and fabrication of a 2-dimensional visible photonic band structure confined within a planar semiconductor waveguide Mater. Sci. Engin. B49 155
J D Joannopoulos, R D Meade and J N Winn 1995 Photonic Crystals: Molding the Flow of Light (Princeton University Press)
M Senechal 1995 Quasicrystals and Geometry (Cambridge University Press)
P R Villeneuve and M Piché 1994 Photonic bandgaps in periodic dielectric structures Prog. Quantum Electron. 18 no12 p153
E Yablonovitch 1987 Inhibited spontaneous emission in solid-state physics and electronics Phys. Rev. Lett. 58 2059
E Yablonovitch and T J Gmitter 1989 Photonic band structure: the face- centered-cubic case Phys. Rev. Lett. 63 1950
M E Zoorob et al. 2000 Complete photonic bandgaps in 12-fold symmetric quasicrystals Nature 404 740
Comprehensive database of photonic-crystal publications and Web resources www.neci.nj.nec.com/homepages/vlasov/photonic.html